고정소수점 방식
고정소수점 방식은 메모리를 정수부와 소수부로 고정으로 나누고 지정하여 처리하는 방식이다.
소수부의 자릿수를 미리 정하고 고정된 자릿수의 소수를 표현하기 때문에 직관적이다.

5.625의 경우
0 000000000000101 1010000000000000
직관적으로 메모리에 실수 표현할 수 있는 장점이 있지만,
표현 가능한 범위가 매우 적다는 단점이 존재 -> -2^15 ~ 2^15-1
123.1 라는 실수가 있을 경우, 0.1 의 숫자를 표현하기 위해 16비트의 소수부 모두를 사용하는 것은 낭비
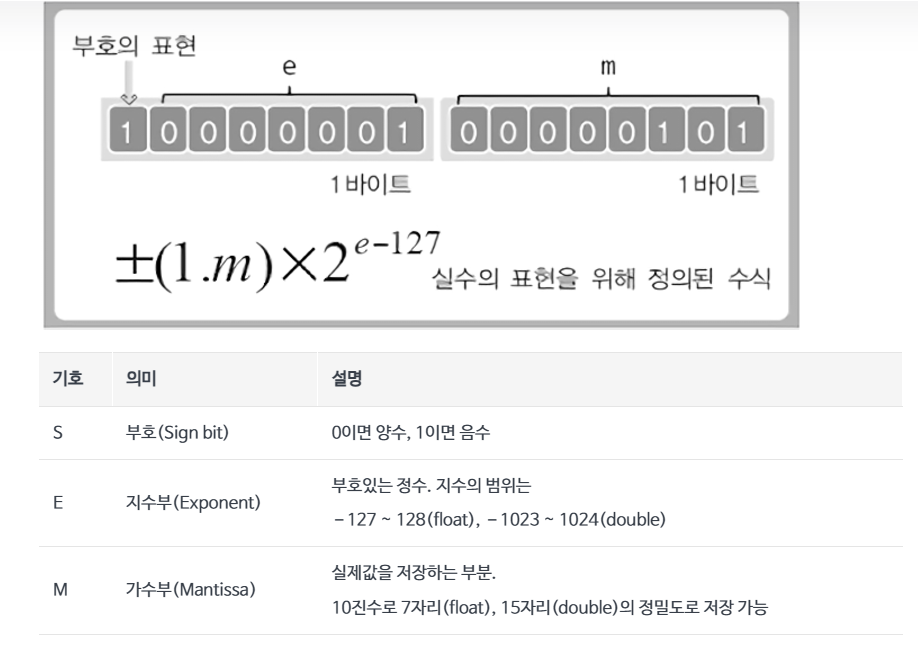
부동소수점 방식
소수점이 둥둥 떠다닌다는 의미로, 표현할 수 있는 값의 범위를 최대한 넓혀 오차를 줄이자는 시도에서 탄생
고정 소수점 방식과는 달리 메모리를 지수부(8bit), 가수부(23bit)로 나눈다.
가수부에는 실제 실수 데이터 비트, 지수부는 소수점 위치를 가리키는 제곱승
고정소수점 방식 : 12.345 (정수.소수)
부동소수점 방식 1.xxx * 2^n (가수 * 지수)
지수(e) 표기법
지수 표기법은 아주 큰 숫자나 아주 작은 숫자를 간단하게 표기할 때 사용되는 표기법으로, 과학적 표기법이라고도 불리운다.
길다란 실수 숫자를 나타내는데 필요한 자릿수를 줄여 표현해준다는 장점이 있다.
double d2 = 1.234e2; // 1.234 * 10^2 = 123.4
double e1 = 1.7e+3; // 1700.0
double e2 = 1.7E-3; // 0.0017
- 소수점이 없을 수도 있음.
- e나 E로 지수부를 시작함.
- +는 생략할 수 있음.
타입 범위 수 long(정수) vs float(실수)
long 타입의 최대 크기인 9223372036854775808 와 float 타입의 최대 크기인 3.4 x 10^38 를 비교해보니 4바이트의 실수형 float 이 훨씬 수의 범위가 큰것을 코드를 통해 확인할 수 있다.
부동소수점 계산 방법
부동 소수점 방식은 대부분 IEEE 754 표준을 따르고 있다.
ex. -118.625라는 실수를 부동 소수점으로 변환
# 정수부 변환
118
= 1110110(2)
# 소수부 변환
0.625
= 0.625 x 2 = 1.250 → 정수부 1
= 0.250 x 2 = 0.500 → 정수부 0
= 0.500 x 2 = 1.000 → 정수부 1
= 101(2)
# 결과
118.625
= 1110110.101(2)`
# 정수부가 한자리가 되도록 변환
1110110.101 → 1.110110101 x 2^6 (지수 = 6)
가수부 비트에 실수값 그대로를 넣는다.(점 무시)

지수에 바이어스 값(127)을 더하고 지수부 비트에 넣는다.

결과

bias를 사용하는 이유 : 지수가 음수가 될 수도 있는 케이스가 있기 때문.
⭐프로그래밍에서의 소수 계산 오차 (무한 소수)
0.625와 같이 이진수 소수점으로 딱 떨어지는 수는 문제없지만, 0.1와 같이 0.0001100110011…(2)로 무한 반복되는 이진수 실수가 문제된다.
즉, 컴퓨터의 메모리는 한정적이기 때문에 실수의 소숫점을 표현할 수 있는 수의 제한이 존재하게 될 수 밖에 없다.
실수를 표현하는 숫자 제한이 있다는 것 -> 부정확한 실수의 계산값
double value1 = 12.23;
double value2 = 34.45;
// 기대값 : 46.68
System.out.println(value1 + value2); // 46.68000000000001
금융 관련 프로그램에서는 이 오차가 큰 영향을 미칠 수 있기 때문에 정확한 값이 필요하다.
JAVA 언어에서는 int, long 정수형 타입으로 치환하고 사용하거나, BigDecimal 클래스를 이용하면 된다.
// int, long 정수형 타입으로 치환
double a = 1000.0;
double b = 999.9;
System.out.println(a - b); // 0.10000000000002274
// 각 숫자에 10을 곱해서 소수부를 없애주고 정수로 형변환
long a2 = (int)(a * 10);
long b2 = (int)(b * 10);
double result = (a2 - b2) / 10.0; // 그리고 정수끼리 연산을 해주고, 다시 10.0을 나누기 하여 실수로 변환하여 저장
System.out.println(result); // 0.1
// BigDecimal 자료형을 사용
BigDecimal bigNumber1 = new BigDecimal("1000.0");
BigDecimal bigNumber2 = new BigDecimal("999.9");
BigDecimal result2 = bigNumber1.subtract(bigNumber2); // bigNumber1 - bigNumber2
System.out.println(result2); // 0.1
반올림하는 것은 정확하지 않다.
앞으로 편리함보단 정확함을 추구하자.