플루이드-워셜(Floyd-Warshall)
다이나믹 프로그래밍 기법을 사용한 알고리즘
음수 사이클이 없는 그래프 내의 모든 정점에서 모든 정점까지의 최단 거리를 구할 수 있는 알고리즘
"인접 행렬을 이용하여 각 노드간 최소 비용을 계산"
음수 사이클 : 사이클의 모든 경로를 지나 원래 지점으로 돌아왔을 때 비용이 음수가 되는 경우
다이나믹 프로그래밍 : 특정 범위의 값을 구하기 위해 다른 범위의 값을 이용하여 효율적으로 찾음
구현 순서
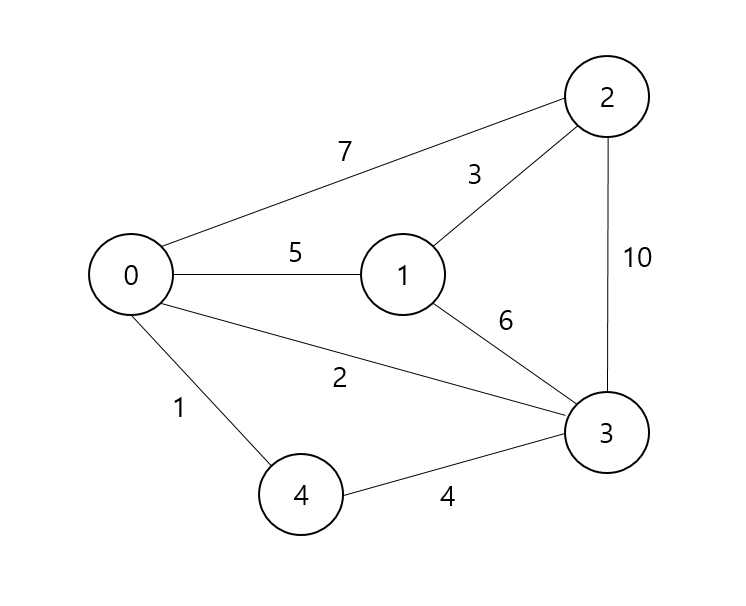
1 . 0개의 간선을 거치는 경우 : 자기 자신으로 가는 경우(0)를 제외하고 모두 가장 큰 값(INF) 로 설정
2 . 1개의 간선을 거치는 경우 : 최소 비용인 것을 선택
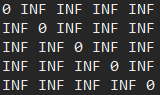
3 . N개의 간선을 거치는 경우 : 2와 동일하게 N개까지
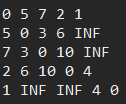
결과

코드 예시
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
/*
sample input(첫 번째 숫자는 노드의 개수, 두 번째 숫자는 간선의 개수 이다).
5
8
0 1 5
0 4 1
0 2 7
0 3 2
1 2 3
1 3 6
2 3 10
3 4 4
*/
public class 플로이드 {
static int N, M;
static int[][] dist;
public static void main(String[] args) throws NumberFormatException, IOException {
// 초기화
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
M = Integer.parseInt(br.readLine());
// 플로이드 초기 거리 테이블 초기화
dist = new int[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
// 자기 자신으로 가는 길은 최소 비용이 0이다.
if (i == j) {
dist[i][j] = 0;
continue;
}
// 자기 자신으로 가는 경우를 제외하고는 매우 큰 값(N개의 노드를 모두 거쳐서 가더라도 더 큰 값).
dist[i][j] = 100_000_000;
}
}
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
// 가는 경로가 하나가 아닐 수 있다. 따라서 그 중 최소 비용을 저장해두면 된다.
dist[a][b] = Math.min(dist[a][b], cost);
dist[b][a] = Math.min(dist[b][a], cost);
}
// 플로이드 워셜 알고리즘
// 노드를 1개부터 N개까지 거쳐가는 경우를 모두 고려한다.
for (int k = 0; k < N; k++) {
// 노드 i에서 j로 가는 경우.
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
// k번째 노드를 거쳐가는 비용이 기존 비용보다 더 작은 경우 갱신
// 또는 연결이 안되어있던 경우(INF) 연결 비용 갱신.
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
// 출력
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
// 연결이 안되어 있는 경우
if (dist[i][j] == 100_000_000) {
System.out.print("INF ");
} else {
System.out.print(dist[i][j] + " ");
}
}
System.out.println();
}
}
}
시간 복잡도
모든 노드(V)에 대해서, V x V 행렬을 갱신해주는 연산을 진행하므로 O(V^3)의 시간 복잡도를 가진다.
입력 값의 크기가 100이라도 100만번의 연산을 수행
참고 URL : https://sskl660.tistory.com/61